Implications of the Asymmetry of g for predictive validity.

Martin G. Evans

Rotman School of Management

&

Department of Psychology

University of Toronto

Poster presented at the APA/Yale Conference on Intelligence, June 2000

Highlights

• Recent evidence that g is asymmetric, being weaker at high levels of intelligence than at low levels of intelligence.
• Implications for the use of g as a predictor of performance.
• • Additive model of g and specific abilities is inadequate.
  • Declining g implies an interactive model between g and specific ability.
• Barriers to the adequate assessment of the multiplicative model (non linear scale transformation, multicollinearity, differential reliability).
• Requirements for further research.

  ---

The underlying assumption in much of the work on intelligence is that, with increasing g, there is increasing ability to do many different things. A number of researchers have recently rediscovered a challenge to this point of view: the so-called Divergence Hypothesis.

The Divergence Hypothesis

History

It was as far back as 1927 that Spearman first noted that g followed a law of diminishing returns (Spearman, 1927: p. 219). He labeled this the divergence hypothesis. This states that at high levels of g, abilities are not as closely associated as they are at lower levels of g. Evans (1999) notes that:

One can visualize this in three dimensions by imagining the various abilities as flowers arranged in a narrow vase - at the bottom, they are bound together tightly, at the top they spread out broadly. (p. 1059)

Despite the enormous amount of research on intelligence and the arguments about whether or not single (Jensen, 1998) or multiple factors (Gardner, 1983) are required to assess intelligence, the divergence hypothesis was lost sight of until fairly recently. This despite the fact that such a hypothesis implies the presence of a single factor at the lower end of the g spectrum and multiple factors at the higher end of the g spectrum.

Results from modern tests

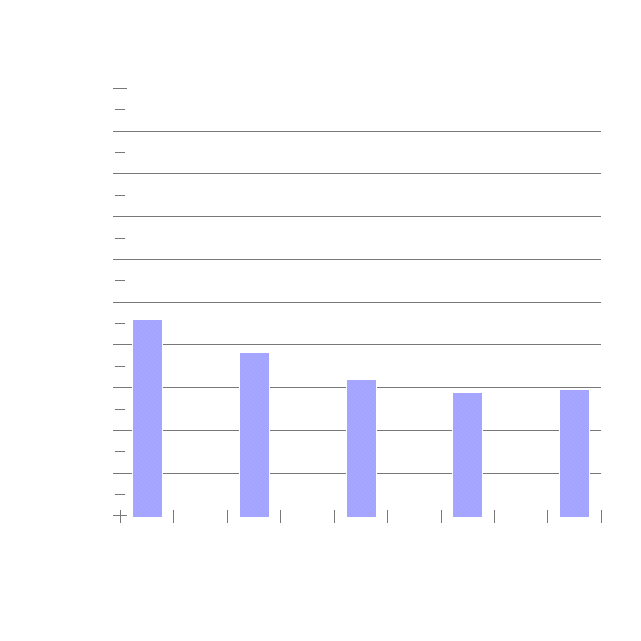
Detterman & Daniel (1989) were the first, albeit inadvertently (Deary & Pagliari, 1991) to rediscover this law of diminishing returns. At high levels of g they found low intercorrelations between tests in the WAIS-R and the WISC-R. Their work was followed by a number of other investigators using a variety of different intelligence tests (ASVAB, DAT-T, etc.). We summarize these in Table 1 and a summary chart (Figure 1) based on a meta-analysis of the data⁽¹⁾. These data show clearly that as g increases, the intercorrelation between the various scales decreases. The pattern is fairly consistent for the many different ways in which g was measured (i.e., how the sample was classified to identify the high and low g groups). This was usually done by rotating through all the scales in the test as the classifier and looking at the correlations between the remaining tests in the high and low groups. Only Evans (1999) tried to find independent assessments of g that were not part of the test battery under investigation. Most authors have argued that classification on scales that are highly g-loaded result in a stronger divergence effect. This meta-analysis does not support this position.⁽²⁾

Implications for predictive validity

If g is no longer homogeneous but becomes less strong as intelligence increases, new implications for the prediction of job performance emerge: at high levels of g, relevant specific abilities may come into their own as predictors.⁽³⁾

Conventional wisdom.

Work over the past decade on validity generalization suggests that a single predictor - intelligence - is associated with performance in a variety of different jobs (Hunter, 1986). This work has been undertaken in large sample studies that included both civilian (Pearlman, Schmidt, & Hunter, 1980) and military occupations (McHenry, Hough, Toquam, Hanson, & Ashworth, 1990; Olea & Ree, 1994; Ree, Earles, & Teachout, 1994).

Differential predictions

There are two ways of exploring differential prediction: an additive model and an interactive multiplicative model. In the additive model, performance would be viewed as a consequence of g and specific abilities (s_s).

Additive Model: ,,,,,,Perf. = Fu (g, s)

In the interactive model, we would expect that g would predict performance when g is low while the s_s would predict performance when g is high. This implies that performance is a function of g*s_s. So the declining positive manifold implies an interactive rather than an additive differential prediction model.

Interactive Model: ,,,,,,Perf. = Fu (g, s, g*s)

There has been some testing of the joint impact of general and specific ability using the additive model. Ree and his associates have been notable in their attempt to examine psychometric g⁽⁴⁾ as a predictor; others (Pearlman et al., 1980; McHenry et al., 1990) have used specific test clusters from well-validated tests. Both groups of researchers find only a small increment in predictive validity for both training scores and performance ratings (r = .02)⁽⁵⁾ when specific ability is added to an equation containing general ability. As these researchers use an additive model, it may not be surprising that the incremental validity is low. The appropriate model, implied by the declining positive manifold, is something quite different: an interactive model in which g is both a predictor of performance and a moderator of the relationship between a specific ability and performance. We expect that the best predictor will be the set: g, task relevant specific ability, and the product of g and the specific ability. When g is low, we would not expect the specific ability(ies) to contribute to predictability, when g is high, we would expect the specific abilities to have additional predictive power.

Barriers to an Assessment of Differential Validity based on the Multiplicative Model.

1. Busemeyer & Jones (1983) argue that the analysis of interaction effects through the typical moderated hierarchical regression (Evans, 1991; Saunders, 1956; Zedeck, 1971) is fatally flawed because there may be nonlinear transformations between the concept and the scale used to measure it. This makes it difficult to unequivocally determine whether or not the multiplicative model is supported by the data. Following their suggestions, (Lubinski & Humphreys, 1990) were the only researchers to specifically test the hypothesis that two types of intelligence might interact in the prediction of performance. In this case, they looked at the suggestion that high mathematical ability and high spatial visualization ability was required for the highest levels of mathematical performance. Although their initial analysis suggested support for this idea in that the product term (mathematics * spatial) added significantly to predictability over and above the main effects (mathematics, spatial), subsequent analysis that looked at the square of mathematical reasoning was found to fit the data better. Of course, the interpretation is ambiguous: the transformation from concept to measure might be nonlinear, or the relation between performance and mathematical ability might be curvilinear (see also the next point).
2. level of correlation between g and specific ability. As the correlation between general and specific abilities increases, it becomes more and more difficult to distinguish between a model incorporating g² and a model incorporating g*s. For example, in the Lubinski and Humphrey's paper correlations between the square of the mathematical test and the product of the mathematical and spatial tests ranges, depending on grade level, between 0.92 and 0.933, This is a very high degree of multicollinearity. It is very likely that order of entry of these two terms is quite unstable. Of course, this concern would not apply to the work of Ree and his coauthors who used the principal (orthogonal) components of the test battery. However, they have yet to undertake a test of the multiplicative model.
3. the differential reliability of intelligence tests at different levels of g. An alternative cause for the observed asymmetry lies in the possibility of differential reliability of the specific abilities at low and high levels of g (Deary & Pagliari, 1991). Deary et al (1996) demonstrated clearly that this was not the case for the British DAT tests. Evans (1999) has argued that this is unlikely to be the case for the Armed Services Vocational Aptitude Battery, but he has no evidence to support this.

Conclusion

This is what is needed for further advance in this area: critical tests of the g only model and of the two incremental validity models, additive and interactive. This will require:

• a range of jobs, some with low job complexity and ability requirements; others with high job complexity and ability requirements⁽⁶⁾. My expectation is that the multiplicative differential effects will only occur in the latter situation.
• measures of general and specific abilities that are:
  • reliable at both ends of the g spectrum
  • for the specific skills, relevant to the jobs for which they are used as predictors
• accurate measures of job performance
• situations where performance is under control of the employee (James, Demaree, Mulaik, & Ladd, 1992).
•  

  ---

References

Abelson, A. R. (1911). The measurement of mental ability of "backward" children. British Journal of Psychology, 4, 269-314.

Busemeyer, J. R., & Jones, L. E. (1983). Analysis of multiplicative combination rules when the causal variables are measured with error. Psychological Bulletin, 93, 549-562.

Deary, I. J., & Pagliari, C. (1991). The strength of g at different levels of ability: Have Detterman and Daniel rediscovered Spearman's "Law of Diminishing Returns"? Intelligence, 15, 247-250.

Deary, I. J., Egan, V., Gibson, G. J., Austin, E. J., Brand, C. R., & Kellaghan, T. (1996). Intelligence and the differentiation hypothesis. Intelligence, 23, 105-132.

Detterman, D. K., & Daniel, M. H. (1989). Correlates of mental tests with each other and with cognitive variables are highest for low IQ groups. Intelligence, 13, 349-359.

Evans, M. G. (1991). The problem of analyzing multiplicative composites: Interactions revisited. American Psychologist, 46, 6-15.

Evans, M. G. (1999). On the asymmetry of g. Psychological Reports, 85, 1059-1069.

Gardner, H. (1983). Frames of Mind: The Theory of Multiple Intelligences. New York, NY: Basic Books.

Hunter, J. E. (1986). Cognitive ability, cognitive aptitudes, job knowledge, and job performance. Journal of Vocational Behavior, 29, 340-362.

James, L. R., Demaree, R. G., Mulaik, S. A., & Ladd, R. T. (1992). Validity generalization in the context of situational models. Journal of Applied Psychology, 73, 3-14.

Jensen, A. (1998). The g factor: The science of mental ability. Westport, CT: Praeger.

Jones, G. E., & Ree, M. J. (1998). Aptitude test score validity: No moderating effect due to job ability requirement differences. Educational and Psychological Measurement, 58, 284-294.

Legree, P. J., Pifer, M. E., & Grafton, F. C. (1996). Correlations among cognitive abilities are lower for higher ability groups. Intelligence, 23, 45-57.

Lubinski, D., & Humphreys, L. G. (1990). Assessing spurious "moderator effects": Illustrated substantively with the hypothesized ("synergistic") relation between spatial and mathematical ability. Psychological Bulletin, 107, 385-393.

Lynn, R. (1992). Does Spearman's g decline at high IQ levels? Some evidence from Scotland. Journal of Genetic Psychology, 153, 229-230.

McHenry, J. J., Hough, L. M., Toquam, J. L., Hanson, M. A., & Ashworth, S. (1990). Project A validity results: The relationship between predictor and criterion domains. Personnel Psychology, 43, 335-354.

Olea, M. M., & Ree, M. J. (1994). Predicting pilot and navigator criteria: Not much more than g. Journal of Applied Psychology, 79, 845-851.

Pearlman, K., Schmidt, F. L., & Hunter, J. E. (1980). Validity generalization results for tests used to predict job proficiency and training success in clerical occupations. Journal of Applied Psychology, 65, 373-406.

Ree, M. J., Earles, J. A., & Teachout, M. S. (1994). Predicting job performance: Not much more than g. Journal of Applied Psychology, 79, 518-524.

Saunders, D. R. (1956). Moderator variables in prediction. Educational and Psychological Measurement, 16, 209-222.

Spearman, C. E. (1927). The Abilities of Man. London, UK: Macmillan.

Zedeck, S. (1971). Problems with the use of moderator variables. Psychological Bulletin, 76, 295-310.

1. Note that the within cell variances were higher than the variance due to sampling error. This is probably a consequence of a) the extremity of the selection, b) the measures used, and c) the classification scales used.

2. One of the highly g-loaded scales in Deary et al. (1996), Analytic Reasoning, showed an "increasing returns" effect. When this was omitted from the high g analysis, the results were no different.

3. My expectation is that this is true when jobs requiring a high level of ability are involved.

4. This is assessed as the first principal component of a factor analysis

5. The use of the components of a principal axis analysis ensures that the general factor is extracted from all scales and that all components extracted are orthogonal. This ensures that subsequent analysis adds unique variance in a regression equation. The use of real tests ensures that meaningful subsets of skill and ability are used, when g is extracted, subsequent components do not seem to reflect particular bundles of competencies; though the use of a Vernon-like hierarchical structure would enable both g and meaningful components to be used - no analyses used this technique.

6. By this I mean the level of ability required, not the kind of ability required which is what is addressed in Jones and Ree (1998)